pH Wert & Verdünnungsreihe
Nützliche Grundlagen – 10. Klasse Überblick:
Zu Berechnungen mit der Thematik pH-Wert in der Mittelstufe (8-11 Klasse) benötigt man folgende Formeln:
- pH = – lg c(H3O+)
- c(H3O+) = 10-pH
Theoretisch kann man die beiden Formeln auch ineinander umformen, jedoch muss man das in der Mittelstufe nicht selbst beherrschen, es reicht die zwei Formeln auswendig zu lernen. Darüber hinaus kann man neben dem pH Wert auch den pOH Wert betrachten. Dann werden anstelle der Oxonium-Ionen die Hydroxid-Ionen in der vorliegenden Lösung betrachtet. Auch für den pOH-Wert gibt es zwei Formeln:
- pOH = – lg c(OH–)
- c(OH–) = 10-pOH
Fragen zum Video (es werden 5 von 9 möglichen Fragen gestellt):
Bei der Verdünnungsreihe handelt es sich um Überlegungen, wie man ein bestimmtes Volumen mit einem Lösungsmittel, hier Wasser, so verdünnen kann, dass der pH-Wert um den Wert 1 steigt. Dafür muss man eine 1:10 Verdünnung anwenden. Wenn ich also 5 mL einer Lösung mit pH = 2 verdünnen möchte, muss ich 45 mL Wasser zugeben, damit daraus eine Lösung mit pH= 3 wird.
Eine Unterscheidung in starke, mittelstarke und schwache Säuren bzw. Basen erfolgt in der Mittelstufe nicht. Alle Säuren und Basen werden hier wie starke Säuren oder Basen behandelt.
FAQ
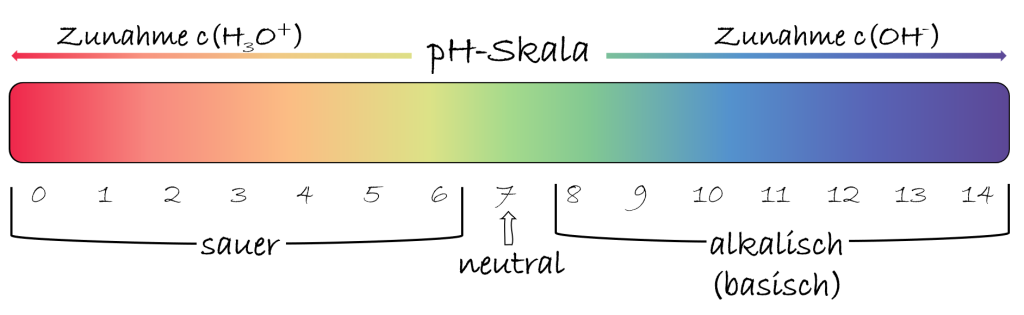
Der pH-Wert ist ein Maß für die Konzentration von Oxoniumionen (H₃O⁺) in einer wässrigen Lösung. Einfacher ausgedrückt zeigt er an, wie sauer oder basisch (alkalisch) eine wässrige Lösung ist. Die pH-Skala reicht in der Regel von 0 bis 14, wobei Werte um 7 als neutral gelten. Werte unter 7 kennzeichnen saure Lösungen, während Werte über 7 basische Lösungen darstellen. Je niedriger der pH-Wert, desto höher die Konzentration an Oxoniumionen und desto saurer ist die Lösung. Umgekehrt gilt: Je höher der pH-Wert, desto geringer die Konzentration an Oxoniumionen und desto basischer ist die Lösung.
In jeder wässrigen Lösung liegen sowohl Oxoniumionen (H₃O⁺) als auch Hydroxidionen (OH⁻) vor. Das Produkt ihrer Konzentrationen ist bei 25 °C konstant und beträgt 10⁻¹⁴ (mol/L)²: c[H₃O⁺] * c[OH⁻] = 10⁻¹⁴. Das bedeutet, dass wenn die Konzentration der Oxoniumionen steigt (die Lösung wird saurer, der pH-Wert sinkt), die Konzentration der Hydroxidionen sinkt, und umgekehrt. Bei einem neutralen pH-Wert von 7 sind die Konzentrationen beider Ionen gleich (jeweils 10⁻⁷ mol/L).
Eine Verdünnungsreihe beschreibt die schrittweise Verringerung der Konzentration einer Lösung durch Zugabe von Lösungsmittel (in der Regel Wasser). Verdünnt man eine saure oder basische Lösung um den Faktor 10 (z.B. indem man zu einem Teil der Lösung neun Teile Lösungsmittel hinzufügt), so ändert sich der pH-Wert um eine Einheit. Bei der Verdünnung einer sauren Lösung um den Faktor 10 steigt der pH-Wert um 1 (die Lösung wird weniger sauer und nähert sich dem neutralen Wert 7 an). Bei der Verdünnung einer basischen Lösung um den Faktor 10 sinkt der pH-Wert um 1 (die Lösung wird weniger basisch und nähert sich ebenfalls dem neutralen Wert 7 an).
Bei mehrprotonigen Säuren, also Säuren, die mehr als ein Proton (H⁺) pro Molekül abgeben können (wie z.B. Phosphorsäure, H₃PO₄), muss das Stoffmengenverhältnis zwischen der Säure und den freigesetzten Oxonium-Ionen berücksichtigt werden. Ein Molekül einer dreiprotonigen Säure wie Phosphorsäure kann in mehreren Schritten bis zu drei Protonen abgeben und somit bis zu drei Oxoniumionen bilden.
Daher ist die Konzentration der Oxoniumionen in einer Lösung einer mehrprotonigen Säure in der Regel ein Vielfaches der Konzentration der ursprünglichen Säure (abhängig von der Anzahl der abgegebenen Protonen und dem Dissoziationsgrad der Säure). Für eine genaue pH-Wert-Berechnung muss die Reaktionsgleichung aufgestellt und das korrekte Stoffmengenverhältnis ermittelt werden, um die tatsächliche Konzentration der Oxonium-Ionen zu bestimmen. Es ist möglich, dass der pH-Wert stark konzentrierter Lösungen mehrprotoniger Säuren auch unter 0 liegen kann.
Nach den Grundlagen seid ihr jetzt für die kommenden Übungen gut gerüstet!


